Computational Fluid Dynamics (CFD) simulations have been used to solve a variety of industrial fluid flow and heat transfer problems. In realistic contexts, in order to obtain suitable numerical results, the fluid behavior, often modeled by Navier-Stokes equations, should be coupled with heat transfer, governed by the energy equations. Industrial applications where such fluid-thermal coupling is numerically simulated have a diverse variety, e.g., heat exchangers, spent fuel storage of nuclear power plants, solar collectors, crude oil storage tanks, energy storage devices, and modern crop dryers [1].
Such a wide span of physical phenomena may be categorized in two different fluid-thermal coupling problems: i) where fluid velocities are considered small and thus the Stokes equation can be used, and ii) with advection-dominated problems with increased velocities, where the full Navier-Stokes equations must be employed.
In our numerical simulations, developed with a C++ in-house code using a Finite Element library named Deal.II, we are investigating the latter, where specific stabilized methods must be used.
The momentum equation of the Navier-Stokes system and the heat equation are both represented with the advection-diffusion equation. The main difference is that, the former is a nonlinear vector value problem, while the latter is a linear scalar problem. Sometimes, when the velocity field increase, some oscillations affect the advection-diffusion equations, and rise up the need to stabilize the solution.
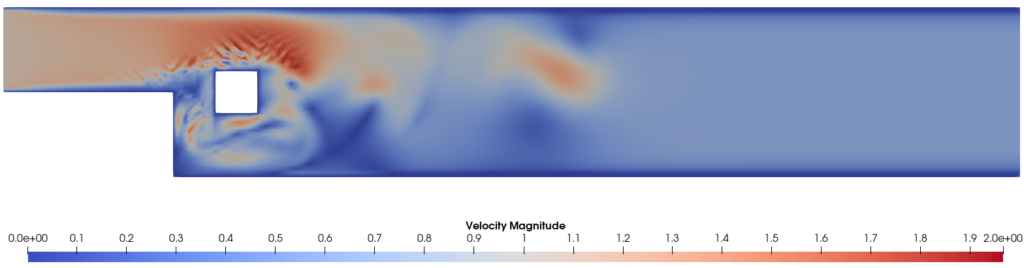
In the figures is shown a comparison between two different approaches used to test the Navier-Stokes equations in order to highlight the effects of high local Reynolds numbers (when inertial forces start to exceed the viscous forces) on the solution.
Fig. 1 depicts the velocity field of the time-dependent linearized approach based on a projection method [2]; here the instabilities affects the solution that presents some waves near the square. In this case the implementation of stabilization technique is required to eliminate the oscillations.
On the other hand, in Fig. 2, the same simulation is carried on solving the nonlinear time-dependent Navier-Stokes equation by means of a modified Newton-Raphson algorithm [3]. Using this approach the residual is minimized more accurately and the solution appears smooth and without winglets.
What concerning the heat equation, the instabilities appear when the advection term is greater than the diffusion term (high Peclet number). In this case we implemented a Streamline Upwind Petrov-Galerkin (SUPG) [4] formulation to avoid some oscillations in the temperature field. As shown in the video below, we are able to represent the advection of the temperature field, coupled with a pulsating velocity field, without instabilities.
Fig. 1: Fluid velocity field obtained solving the Navier-Stokes equations with a linearized approach based on a projection method.
Fig. 2: Fluid velocity field obtained solving the Navier-Stokes equations with a modified Newton-Raphson algorithm.
This work is still in an embryonic phase, but the numerical results obtained so far show the effectiveness of the proposed numerical method, which is able to deliver solutions in excellent agreement with literature benchmark [5].
This work is carried out by the CompMech Group (University of Pavia) members Eng. M. Murer, Dr. S. Morganti and Prof. F. Auricchio together with the researchers of Roma Tre University Dr. F. Milicchio and Prof. G. Formica.
References:
[1] Roychowdhury, D. G., Sarit K. Das, and T. Sundararajan. “Numerical simulation of natural convective heat transfer and fluid flow around a heated cylinder inside an enclosure.” Heat and mass transfer 38.7-8 (2002): 565-576.
[2] Guermond, Jean-Luc, Peter Minev, and Jie Shen. “An overview of projection methods for incompressible flows.” Computer methods in applied mechanics and engineering 195.44-47 (2006): 6011-6045.
[3] Aoussou, Jean, Jing Lin, and Pierre FJ Lermusiaux. “Iterated pressure-correction projection methods for the unsteady incompressible Navier–Stokes equations.” Journal of Computational Physics 373 (2018): 940-974.
[4] Brooks, Alexander N., and Thomas JR Hughes. “Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations.” Computer methods in applied mechanics and engineering 32.1-3 (1982): 199-259.
[5] Selimefendigil, Fatih, and Hakan F. Oztop. “Control of laminar pulsating flow and heat transfer in backward-facing step by using a square obstacle.” Journal of heat transfer 136.8 (2014).
April 24th, 2020