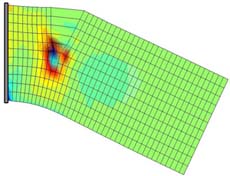
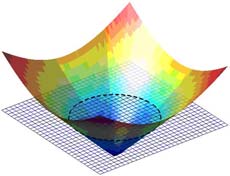
In daily life bodies are subjected to various different kinds of forces. These forces cause stresses in the body. When the stresses exceeds certain threshold limit, progressive failure results. These failures are often initiated by surface or near surface cracks. These cracks lower the strength of the material and hence strength beyond conventional strength is needed. Fracture mechanics is evolved to estimate the resistance of cracked bodies such as civil engineering structure, pressure vessels, automobile components and castings, biomechanics etc. Modeling discontinuities and singularities in the approximating space has been remained a challenge in the world of computational mechanics. The standard Finite Element Method when employed for modeling problems containing discontinuities such as cracks, material interfaces, high gradients etc. , poses a problem in a sense that the FEM mesh is required to conform with the geometry of the discontinuity. Additionally in order to capture high gradients in the approximating field, significant refinement in the vicinity of the discontinuity is required. Above all modeling discontinuities evolving in time with FEM is burdensome due to the need to update the mesh to match the geometry of the discontinuity. This also increases the computational cost. To alleviate the shortcomings associated with meshing of cracks using FEM, Partition of Unity Methods(PUM) were developed. XFEM is a partition of unity based enriched/extended finite element method. The finite element method is used as base in XFEM, and hence large body of the finite element method can be readily exploited. The Extended Finite Element Method exploits the partition of unity property of finite elements as identified by Melenk & Babuska, which allows local enrichment functions to be easily incorporated in the FEM approximation. As the name implies, the standard FEM approximation space is extended or enriched using an appropriate enrichment function, which can best describe the field. Additional functions which might contain any prior knowledge/information about the solution can be incorporated into the finite element space using partition of unity and the resulting space is capable of capturing the local features of interest. For crack modeling a discontinuous jump function and asymptotic near tip displacement fields are added to the displacement-based finite element approximation. The whole beauty of XFEM lies in subdividing the problem into two parts A) generating mesh without cracks/inclusions etc. B) enriching the FEM approximation with additional/enrichment functions that models the discontinuities. This avoids the need for remeshing or explicit geometric modeling of the discontinuity. In general XEM can be used to model cracks, contact and interface problems, simulation of inclusions and holes, moving discontinuities, biphase flow problems, fluid structure interaction etc. Within the framework of XFEM another development is the use of Level set functions for representing discontinuities. Where the discontinuity is represented as a zero Level set function. In the following, some figures showing some of the obtained results are reported.
Fig. 1: Deformed Shape of a Rectangular plate with an initial edge crack.
Fig. 2: Displacement uy of a plate with an edge crack.
Fig. 3: Stress plot σyy of Rectangular plate with an initial edge crack.
Fig. 4: Cantilever Beam with an initial edge crack.
Fig. 5: Discontinuous near-tip Enrichment Function.
Fig. 6: Level Set Function for evolving circular discontinuity.
Fig. 7: Level Set function for two evolving discontinuities.