Isogeometric Analysis is a Galerkin, isoparametric, exact geometry approach, which is recently providing very promising results as an alternative to traditional analysis techniques based on the finite element method. The basic idea consists of the use of typical functions used in CAD systems (such as Non-Uniform Rational B-Splines – NURBS) for both the geometry and the shape functions. The double aim of this choice is to avoid geometry approximations given by the introduction of a mesh (as it typically happens in FEM) and to take advantage of the high regularity of those functions.
The application of isogeometric analysis has already provided very good results in several fields. In particular, within this group, such a technique has been successfully employed for the study of structural vibrations, wave propagation, static structural problems in small and large deformations, and turbulence in fluids.
In the following, a couple of figures showing some of the obtained results are reported.
Clearly, the normalized exact solution is the constant equal to 1.
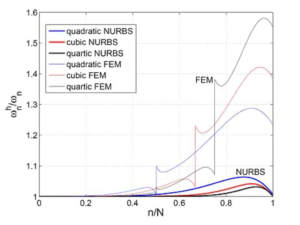
Fig. 1: 1D structural vibrations: comparison of normalized spectra obtained, for different approximation degrees, with isogeometric analysis (NURBS) and with finite element analysis (FEM).
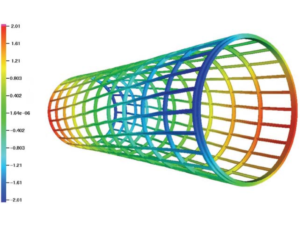
Fig. 2: NASA Aluminum Testbed Cylinder vibration analysis: first torsional mode computed by isogeometric analysis.

