Introduction
Firstly introduced in 2005 [R1], Isogeometric Analysis (IgA) employs typical functions from Computer Aided Design (such as, e.g., NURBS) for describing both geometry and field variables, in an isoparametric fashion [R2, R3]. This leads to exact geometrical representations, typically combined with a superior accuracy per degree of freedom with respect to standard numerical techniques like classical finite elements. Since accurate results deriving from very precise geometrical descriptions and reduced computational times are key ingredients of computer-based simulations, especially in the field of predictive biomedicine, we aim at showing the suitability of innovative isogeometric techniques for the simulation of complex problems such as the behavior of aortic valves.
Goal
The purpose of the present work is to develop simple and accurate modeling and analysis procedures for the simulation of aortic valves. To accomplish this goal, we believe that the use of isogeometric analysis may represent a big advantage over standard finite element techniques.
Method
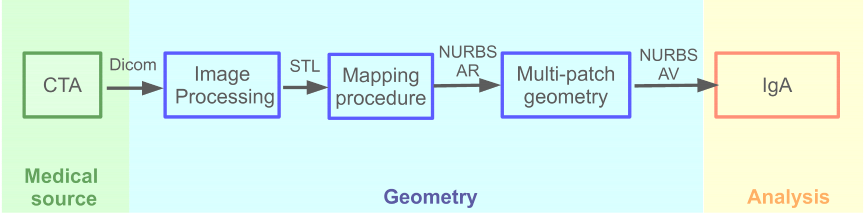
Briefly stated, starting from contrast-enhanced CTA images, we obtain a stereolitographic representation (STL) of the aortic root, which is used as target object to generate an isogeometric patient-specific model through a mapping procedure. Aortic leaflets, not visible with CTA, are constructed by integrating CTA data and ultrasound information, completing, thus, the creation of the aortic valve multi-patch structure. The diastolic behavior of the considered aortic valve is finally reproduced through isogeometric analysis. Finally, results obtained throuogh IgA are compared with those obtained through standard finite elements. The approach developed to perform patient-specific IgA of the aortic valve is sketched in the following flowchart.
Results
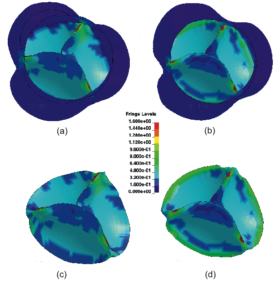
Fig. 2: Von Mises stress pattern: (a) isogeometric analysis of valve closure (762 control points); (b) finite element analysis of valve closure (37972 nodes); (c) a focus on the isogeometric leaflet model (762 control points); (d) a focus on the finite element leaflet model (37972 nodes).
References
- [R1] T.J.R. Hughes, A.J. Cottrell, and Y. Bazilevs. Isogeometric analysis: CAD, finite el- ements, NURBS, exact geometry, and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194:4135–4195, 2005.
- [R2] J.A. Cottrell, T.J.R. Hughes, and Y. Bazilevs. Isogeometric Analysis: Toward Integration of CAD and FEA. John Wiley and sons, 2009.
Group publications
- [P1] J.A. Cottrell, T.J.R. Hughes, and A. Reali. Studies of refinement and continuity in isogeometric structural analysis. Computer Methods in Applied Mechanics and Engineering, 196:4160–4183, 2007.