HomeResearch activitiesCivil EngineeringMixed models for the structural analysis

Mixed models for the structural analysis

Introduction

In the most of Finite Element analysis performed by practitioners, displacement-based beam and plate models are used. Unfortunately, these models must often be corrected by shear factors, suffer from locking phenomena, and generally give a low accurate stress description. By the contrary, it is possible to set up mixed beam and plate finite elements (in which also stresses and strains are considered as independent variables) which are generally locking-free and give a more accurate stress description. Unfortunately these (sometimes called “exotic”) models could be not compatible with classical ones, use a non-conform formulation, and stability problems lead often the methods to be extremely complicated to manage.

Goal

Our purpose is to look for a new development pathway that takes the best properties of both approaches while minimizing and controlling the disadvantages.

Methods

Starting from the 3D formulation fo the elastic problem, the aim is to be able to operate a “dimensional reduction of the problem”, obtaining the 1D beam model or the 2D plate model. As a second step, it is then possible to develop suitable 1D or 2D Finite Elements or apply other numerical techniques.

Results

Planar beam

Fig. 1: Stresses σx(x) and τ(x) of a three layer, homogeneous cantilever, clamped in x = 0, loaded in the opposite extremity by a quadratic shear distribution and modeled by means of 64 elements. It is evident that the model under investigation is able to catch the boundary effects of bounded extremity.

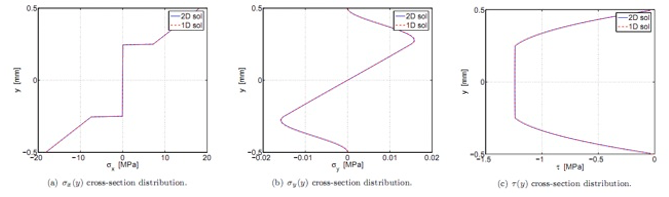
Fig. 2: Comparison of section stress distribution in a laminated beam. The red dotted line is the solution obtained from the beam model, the blue continue one is the overkilled solution of the planar problem under investigation.

3D beam

Fig. 3: Shear cross-section distributions (a) and (b) and cross-section error distributions (c) and (d) for the case of a cantilever loaded with a vertical load with an homogeneous and square cross section.

Plate

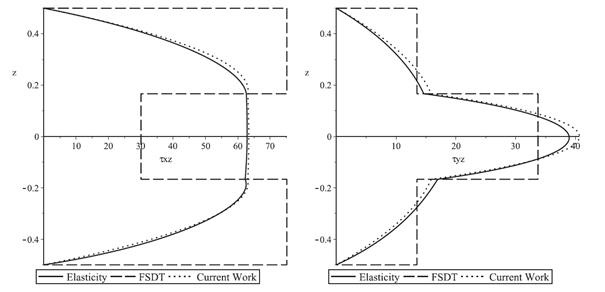
Fig. 4: Out of plane shear stresses ?xz and ?yz evaluated for 3 layers, non homogeneous, orthotropic, square, and simply supported plate, fiber orientation 0/90/0, distribution along the thickness. Elasticity is the analytical solution (see Pagano 1970), FSDT in the First Order Deformation Theory, Current Work is the proposed model.

Non-prismatic beam

Fig. 5: Results of “S12” obtained by using the software Abaqus for the cantilever curvilinearly tapered symmetric beam with a concentrated load on the right edge.

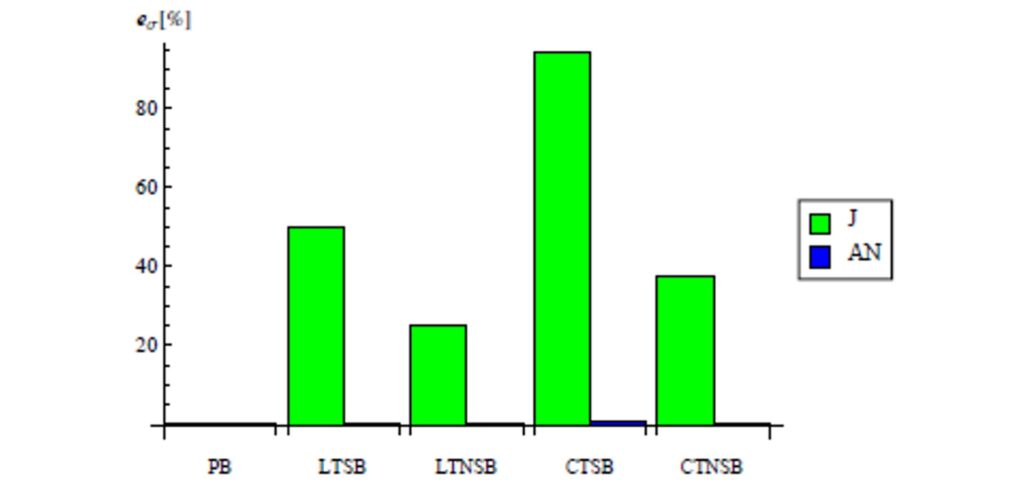
Fig. 6: Percentage error of the shear stress results evaluated with respect to the FE solution. The labels, J and AN, indicate the Jourawsky and the analytical solutions. The labels, PB, LTSB, LTNSB, CTSB and CTNSB, indicate prismatic beam, linearly tapered symmetric beam, linearly tapered non-symmetric beam, curvilinearly tapered symmetric beam and curvilinearly tapered non-symmetric beam, respectively.

Main Collaborations

  • Dipartimento di Matematica “Felice Casorati” Università degli studi di Pavia
  • Institut für Mechanik der Werkstoffe und Strukturen TU Wien

References

  • S. M. Alessandrini, D. N. Arnold, R. S. Falk, and A. L. Madureira, “Derivation and justification of plate models by variational methods”, pp. 1–20 in Plates and shells (Quebec, 1996), edited by M. Fortin, CRM Proc. Lecture Notes 21, Amer. Math. Soc., Providence, RI, 1999.
  • F. Auricchio and E. Sacco, “A mixed-enhanced finite-element for the analysis of laminated composite plates”, Int. J. Numer. Methods Eng. 44 (1999), 1481–1504.
  • F. Auricchio, C. Lovadina, and A. L. Madureira, “An asymptotically optimal model for isotropic heterogeneous linearly elastic plates”, M2AN Math. Model. Numer. Anal. 38:5 (2004), 877–897.
  • E. Reissner, “On a variational theorem and on shear deformable plate theory”, Int. J. Numer. Methods Eng. 23 (1986), 193–198.

Group publications