A comparison between Transformation Field Analysis and Hashin-Shtrikman type techniques
Heterogeneous materials are nowadays used in many engineering applications e.g. constructions, aerospace and automotive. In manufacturing it can be convenient to use materials with an heterogeneous microstructure in order to obtain components with desired material properties. As a consequence, it is important to take the microscopic structure characterized by nonlinear behaviour into account and couple it with the macroscopic response via multiscale analysis.
Numerical multiscale schemes as the well known FE2 have proven to be accurate but computationally expensive. An effective way to decrease the numerical effort of multiscale modelling is to introduce Reduced Order Methods based on data analysis and clustering as the Transformation Field Analysis (TFA) [1].
Our CompMech member Alfredo Castrogiovanni, under the supervision of Prof. Ferdinando Auricchio and in collaboration with Prof. Elio Sacco (Università degli Studi di Napoli Federico II) and Prof. Sonia Marfia (Università di Roma Tre), is working on a Hashin-Shtrikman (HS) type semi-analytical Reduced Order Method [2] extended to plasticity with isotropic hardening.
This method, in contrast with TFA, includes the introduction of an elastic reference material at the micro-level, coupled to the real multi-phase nonlinear material via a eigenstress field. The Representative Volume Element (RVE) is divided in regions, called subsets; these may coincide with the material phases as in the Uniform Transformation Field Analysis (UTFA) or can be refined as in Piecewise Transformation Field Analyses (PWTFA). In both Reduced Order Methods, Hashin-Shtrikman and TFA, the local constitutive equation is evaluated once per subset with clear benefits on the computational burden.
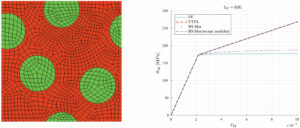
Both methods have been applied to a periodic RVE composed by two materials (Fig. 1, left) proving that under prescribed circumstances the reduced order homogenization techniques are able to reproduce the overall behaviour of the composite. The HS and TFA results are compared to nonlinear finite element results (Fig. 1, right).
References
[1] Dvorak, G., Transformation field analysis of inelastic composite materials. Proc. Roy. Soc. Lond. A 437, 311–327, 1992. [2] S. Wulfinghoff, F. Cavaliere, S. Reese, Model order reduction of nonlinear homogenization problems using a Hashin–Shtrikman type finite element method, Comput. Methods Appl. Mech. Engrg. 330, 149–179, 2018.
June 4th, 2020

