Despite the accelerated deployment of laminated composites in a wide variety of markets due to their peculiar engineering features, the design of those materials is often restrained by the lack of cost‐efficient modeling techniques. In fact, the existing strategies allowing for cheap simulations usually fail to directly capture out-of‐plane through‐the‐thickness stresses, which prove to be typically responsible of delamination failure modes.
Our CompMech Group member Alessia Patton, together with Dr. Pablo Antolin, Dr. John-Eric Dufour, Prof. Josef Kiendl, and Prof. Alessandro Reali, developed a fast and accurate stress recovery strategy to model the out‐of‐plane behavior of Kirchhoff laminated plates. The proposed technique, recently published in Composite Structures, can be regarded as a two‐step approach: First, the classical composite plates theory, providing the lowest computational cost among known literature strategies, is applied to obtain a coarse displacement solution; afterwards, this solution is used to compute the necessary in‐plane derivatives to recover the out‐of‐plane stresses directly imposing equilibrium in strong form. Since this a posteriori step relies on high‐order in‐plane continuity requirements, isogeometric analysis represents a natural simulation framework given its accuracy and higher continuity properties. Both isogeometric Galerkin and collocation formulations are successfully investigated and the effectiveness of the proposed approach is proven by extensive numerical tests.
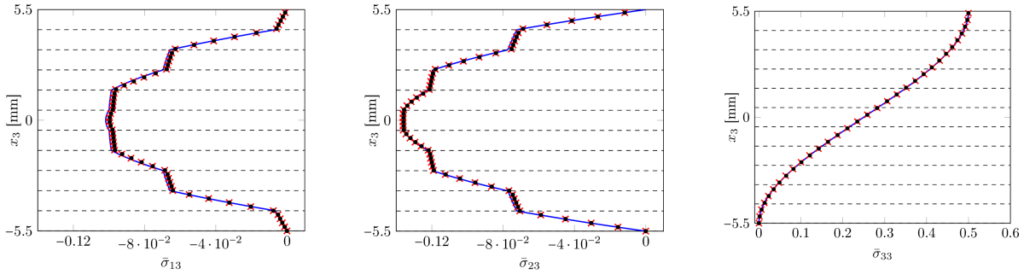
Fig. 1: Through-the-thickness recovered out-of-plane stress solution for the Pagano problem evaluated at x1 = x2 = 3L/4. Plate case with 11 layers and length-to-thickness ratio S = 20 (― Pagano’s analytical solution versus post-processed numerical solutions obtained with degree of approximation p = q = 6, and 7×7 control points: X IGA-Galerkin, • IGA-Collocation).
November 12th, 2020