Multiphysics problems are becoming increasingly popular in Research and engineering applications. Such simulations have been given great attention over the last two decades. Particularly Fluid-structure interaction (FSI) simulation, on which engineering applications are relying to solve problems within aerospace industry, biomedical applications, civil engineering, etc.
In general, a wide range of commercial software rely on partitioned approach for FSI problems to maintain the modularity of their solvers. For example, the commercial software, Ansys, allows the exploitation of each dependent solver capabilities, where the system of equations is solved in a staggered manner, and each output data is transferred back and forth each solver using a specific numerical method to ensure the respect of the interface conditions. However, this can become a bottleneck for problems with high nonlinearities, such as interactions between light structures with incompressible fluids.
We want to compare two approaches for solving a fluid-structure interaction simulation of a pressure wave for an incompressible fluid in an elastic tube. The test case arises in the modelling of the blood flow in large arteries. However, it has not a physiological meaning, since it is generally known that a heartbeat period lasts about 1 second as mentioned by [2]
The numerical example has been previously studied by [[1], [3], [4]]. The results obtained are compared with the results of mentioned references.
The coupled system is solved using partitioned approach using Ansys software capabilities. The structural model is implemented in Ansys Mechanical; the fluid model is developed within Ansys Fluent, and the coupled system is solved using System-Coupling.
The challenge arising in these nonlinear coupled systems is the setup of the coupling algorithms capable of providing accurate and fast convergence. Mainly, the challenge becomes difficult to face when the structure is light, especially if the fluid and solid densities are of the same order. Particularly when density ratio is close or equal to one. In this case, high added-mass effect for incompressible fluids may affect stability and lead to convergence issues. To overcome this issue, numerical methods for partitioned problem has been developed to enhance stability and accelerate convergence. In this study, we compare the Quasi-Newton stabilization method with the classical fixed-point based method.
For comparison purposes, Table 1 gives solution time for each solver, over the entire simulation, and the relative duration of the simulations, for both fixed-point method with constant relaxation parameter (ω = 0.05) and Quasi-Newton stabilization method. In every time-step, the convergence criterion of the coupled problem is set to 10-4.
| Timing summary | QN-LS [sec] | Fixed point (URF) [sec] |
| Coupling time | 985,50 | 3226,2 |
| Fluid solver (Fluent) | 919,32 | 4806,4 |
| Structural solver (Mechanical) | 1232,4 | 10383 |
| Total time | 3137,2 | 18416 |
| Algorithm | N’ iterations/time-step | Average duration |
| QN-LS | ~ 9 | 31,37 sec |
| Fixed-point | ~ 80 | 184,16 sec |
| Ratio (URF/QN) | 8,88 | 5,87 |
Table 1: CPU time of solvers for the coupling methods.
Table 2: Average number of partitioned iterations per time step.
Table 1 indicates that the total computational time for QN-LS method is about six times faster than the fixed-point method. The results show the efficiency and superiority of the QN-LS method in terms of computational time.
Table 2 shows the number of coupling iterations per time-step and relative duration of the simulation. Let us note that the number of solver evaluations per time step has been averaged over the entire simulation.
This shows the superior performance of the Quasi-Newton method which can be exploited for more complicated geometries or tighter convergence criterions.
A few numerical results are illustrated below. Pressure contours on the fluid-structure interface are shown in Figure 1 at different simulation times. The contour plots for both methods agree well with [1] and the corresponding references.
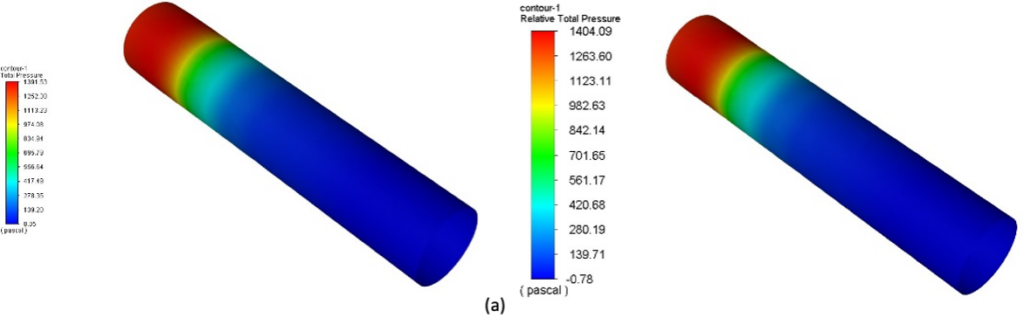
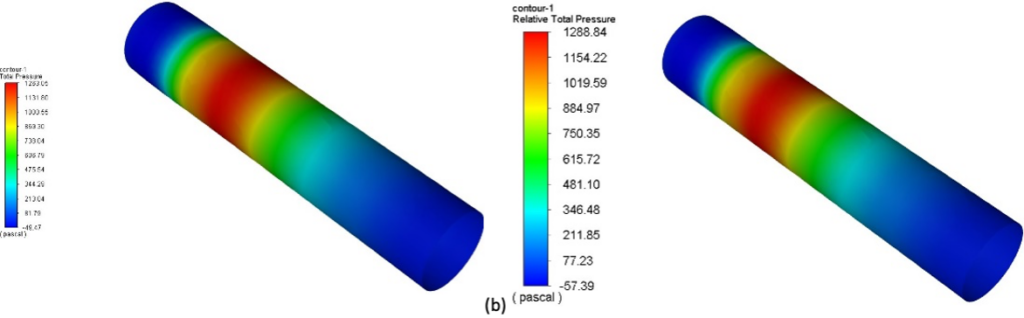
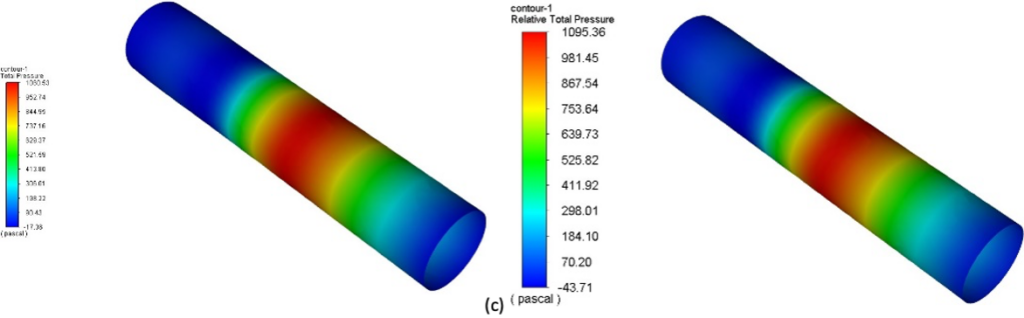
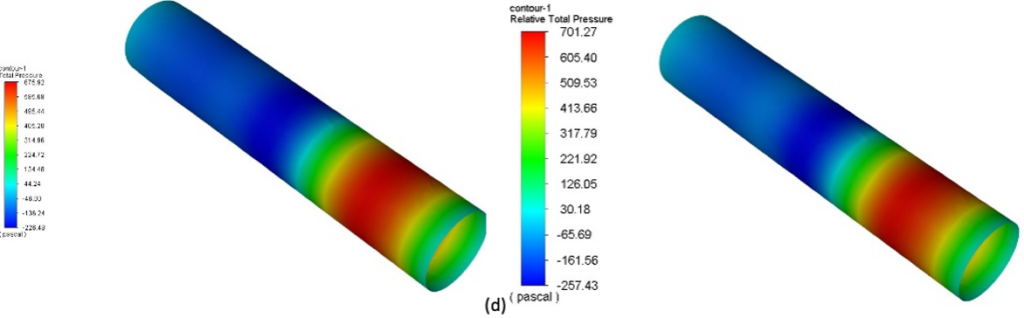
Fig. 1: Pressure contour plots at different time-steps for fixed point (left) and Quasi-Newton (right) coupling algorithms: (a) t = 2.5 ms, (b) t = 5.0 ms, (c) t = 7.5 ms, (d) t = 10 ms.
We plot the evolution of deformation at the center of the tube inner wall, as illustrated in Figure 3, and compare the results against [3].
The results shown in Figure 3 (left) for both fixed-point with constant under-relaxation factor agree with the results obtained by [3] and its corresponding references.
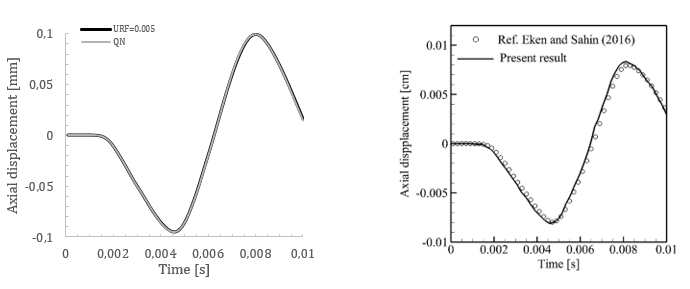
Fig. 3: Comparison of the movement of the point in the center of the elastic tube inner wall; axial displacement.
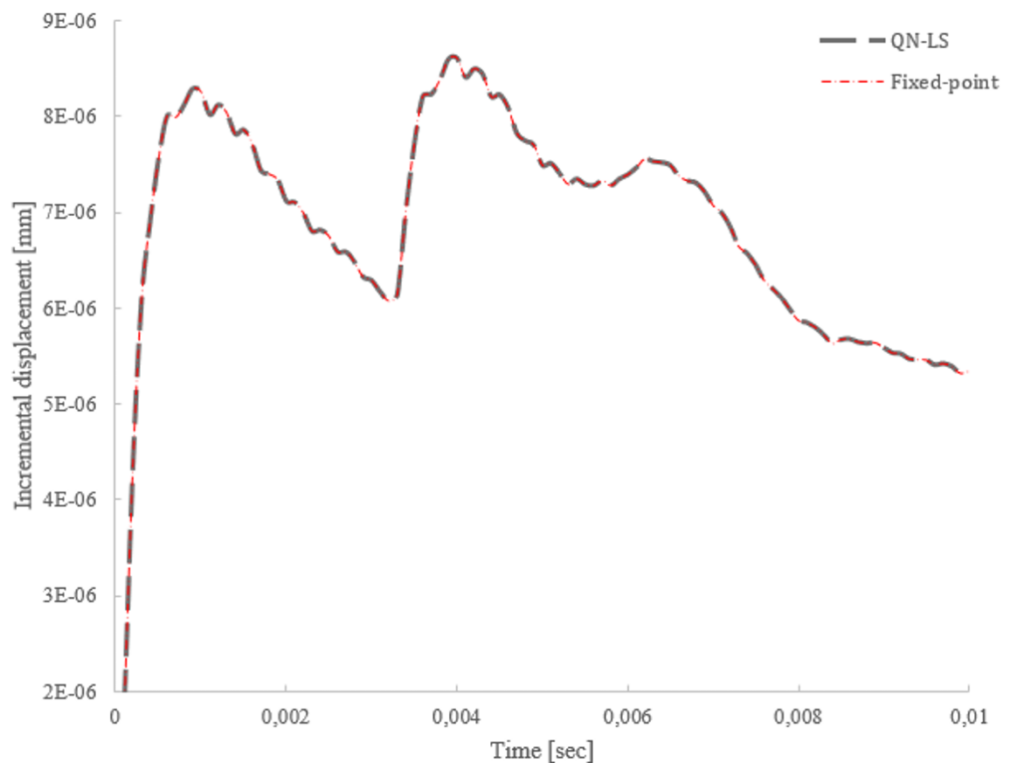
Fig. 4: Maximum incremental displacement through time on the structural elastic tube. Blue: Quasi-Newton method; Red: Fixed-point constant URF.
Although the mesh used in this study is medium, we observe a good agreement of the axial displacement and radial displacement plots against the results obtained by [3].
Finally, a comparison between the two methods as shown in Figure 4 shows a good agreement since the two methods are matching perfectly considering the convergence criterion.
References
[1] J. Degroote, R. Haelterman, S. Annerel, P. Bruggeman, and J. Vierendeels. “Performance of partitioned procedures in fluid–structure interaction”, Computers & Structures (2010) – DOI: 10.1016/j.compstruc.2009.12.006
[2] Miguel Ángel Fernández,Marwan Moubachir. “A Newton method using exact jacobians for solving fluid–structure coupling”, Computers & Structures (2005) – DOI: 10.1016/j.compstruc.2004.04.021
[3] S. T. Ha and H. G. Choi. “Investigation on the effect of density ratio on the convergence behavior of partitioned method for fluid–structure interaction simulation”, Journal of Fluids and Structures (2020) – DOI: 10.1016/j.jfluidstructs.2020.103050
[4] J. Degroote, A. Swillens, P. Bruggeman, R. Haelterman, P. Segers, and J. Vierendeels. “Simulation of fluid–structure interaction with the interface artificial compressibility method”, International Journal for Numerical Methods in Biomedical Engineering (2010) – DOI: 10.1002/cnm.1276
February 24th, 2021

