High-order methods are yet not widely used in engineering applications due to their increased computational cost.
Alexandros Karkoulias is enrolled in the PhD program “Simulation in Engineering and Entrepreneurship Development” (SEED), an Erasmus Mundus Joint Doctorate program that aims at the development of advanced numerical techniques for the modelling and solution of engineering problems. He is carrying out his research at the Polytechnic University of Catalonia (UPC) and the University of Pavia (UNIPV).
The first two years of the program were spent in the Laboratory of Mathematical and Computational Modeling (LaCaN) in the Polytechnic University of Catalonia (UPC) under the supervision of Prof. Antonio Huerta and Dr. Matteo Giacomini. During this period, we focused on the development of an in-house software for fluid dynamics simulations. This software is based on the hybridisable discontinuous Galerkin (HDG), a special type of discontinuous Galerkin (DG) method [1,2].
Currently, as a part of the Computational Mechanics & Advanced Materials Group, the research is supervised by Prof. Ferdinando Auricchio and Dr. Alexander Viguerie. Making use of the potential of linear algebra [3] we are capable of reducing drastically the computational time of the proposed high-order method and thus making it suitable for real-life applications. Maintaining the same levels of accuracy is of high importance, therefore it must be always guaranteed.
The constructed numerical method can be compared with widely used low-order methods and can compete in terms not only of accuracy, but also of computational time.
Afterwards, the aforementioned method can be utilised to simulate fluid flows, an example of which is the flow inside a microvalve, shown in Figure 1. This type of passive microvalve with no-moving parts is used for controlling a microscale flow. The valve facilitates the forward flow over the reverse flow.
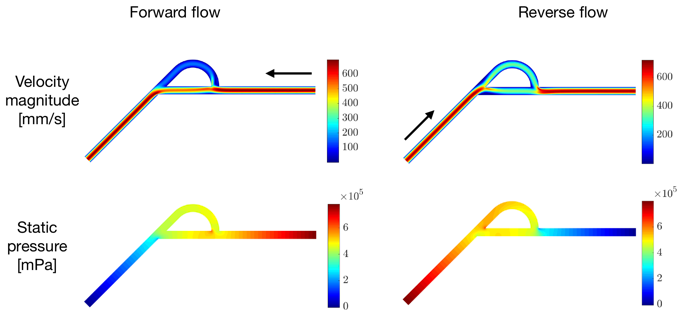
Fig. 1: Velocity and pressure contour of the flow inside a passive microvalve with no-moving parts.
References:
[1] Giacomini, M., Karkoulias, A., Sevilla, R., & Huerta, A. (2018). A superconvergent HDG method for Stokes flow with strongly enforced symmetry of the stress tensor. Journal of Scientific Computing, 77(3), 1679-1702.
[2] Sevilla, R., Giacomini, M., Karkoulias, A., & Huerta, A. (2018). A superconvergent hybridisable discontinuous Galerkin method for linear elasticity. International Journal for Numerical Methods in Engineering, 116(2), 91-116.
[3] Rebholz, L., Viguerie, A., & Xiao, M. (2019). Efficient nonlinear iteration schemes based on algebraic splitting for the incompressible Navier-Stokes equations. Mathematics of Computation, 88(318), 1533-1557.
May 13th, 2019

