On May 15th, our CompMech member, Sai Chandana Divi, published an article on Error-estimation-based adaptive integration for immersed isogeometric analysis in the special issue of Computers and Mathematics with Applications (CAMWA), dedicated to Prof. Ernst Rank’s 65th birthday. The research work for the article was conducted in collaboration with Eindhvoen university of technology (TU/e) under the supervision of Dr. Clemens V. Verhoosel, Prof. E. Harald van Brummelen, Prof. Alessandro Reali, and, Prof. Ferdinando Auricchio. It is sponsored by Erasmus Mundus under join doctorate program called Simulation Engineering and Entrepreneur Development (SEED).
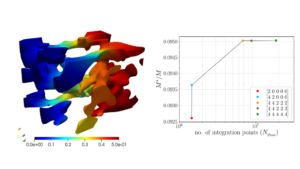
The article focuses on improvising the integration scheme in the context of the Finite Cell Method (FCM) and Isogeometric analysis (IGA). The FCM together with IGA has been applied successfully in various problems in solid mechanics, in image-based analysis, fluid-structure interaction and in many other applications. A challenging aspect of the isogeometric finite cell method is the integration of cut cells. In particular in three-dimensional simulations the computational effort associated with integration can be the critical component of a simulation. A myriad of integration strategies has been proposed over the past years to ameliorate the difficulties associated with integration, but a general optimal integration framework that suits a broad class of engineering problems is not yet available. In this article, Sai provided a thorough investigation of the accuracy and computational effort of the octree integration scheme. She quantified the contribution of the integration error using the theoretical basis provided by Strang’s first lemma. Based on this study she proposed an error-estimate-based adaptive integration procedure for immersed isogeometric analysis. Additionally, she presented a detailed numerical investigation of the proposed optimal integration algorithm and its application to immersed isogeometric analysis using two- and three-dimensional linear elasticity problems.
May 27th, 2020

