The Finite Cell Method (FCM) together with Isogeometric analysis (IGA) has been applied successfully in various problems in solid mechanics, in image-based analysis, fluid-structure interaction and in many other applications. Couple of the key contributors of the FCM and IGA community, Prof. Alexander Düster and Dr. Clemens V. Verhoosel, visited Pavia on February 10th. In this occasion, our CompMech group has arranged a one-day workshop on the current challenges in FCM, especially focused on the issues like integration, application to Additive manufacturing and high Reynolds number flow problems.
The workshop started with a talk from Prof. Alexander Düster, one of the fathers of FCM, on the introduction of Finite Cell Method and presented his work on the Numerical investigation of Polymer Coated Nanoporous Gold.
Our CompMech member, Massimo Carraturo, presented his work on Application of FCM in Additive Manufacturing process control. This work was carried out during his stay at the National Institute of Standard and Technology (NIST, Gaithersburg, MD, USA), together with Dr. Brandon Lane and Dr. Ho Yeung, and supervised by Dr. Stefan Kollmanssberger, Prof. Ernst Rank, Prof. Alessandro Reali, and, Prof. Ferdinando Auricchio.
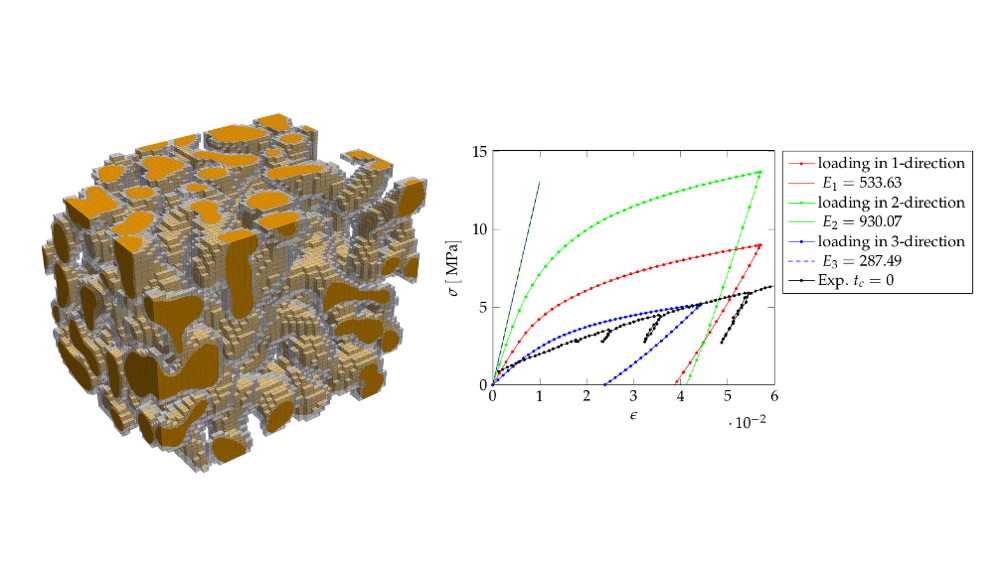
Fig. 1: Polymer coated nanoporous gold and the stress-strain curve
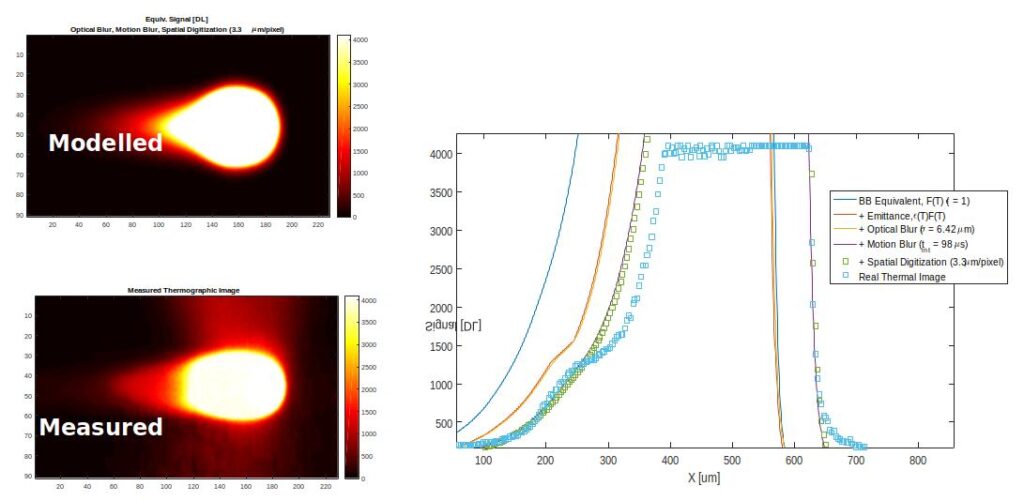
Fig. 2: Modelled vs Measured thermographic image of additive manufacturing
In the afternoon section, Dr. Clemens V. Verhoosel presented the work of Sai Chandana Divi, a joint doctoral candidate of Eindhoven University of Technology and University of Pavia, on further improvements in the integration using Error-estimate based adaptive integration scheme for scan-based simulations. This work is submitted to a special edition of CAMWA. It is supervised by Clemens Verhoosel himself, Prof. E. Harald van Brummelen, Prof. Alessandro Reali, and Prof. Ferdinando Auricchio.
Finally, Sai Chandana Divi presented her recent work on implementation of the method along with Skeleton stabilized formulation for high Reynold’s number flow problems.
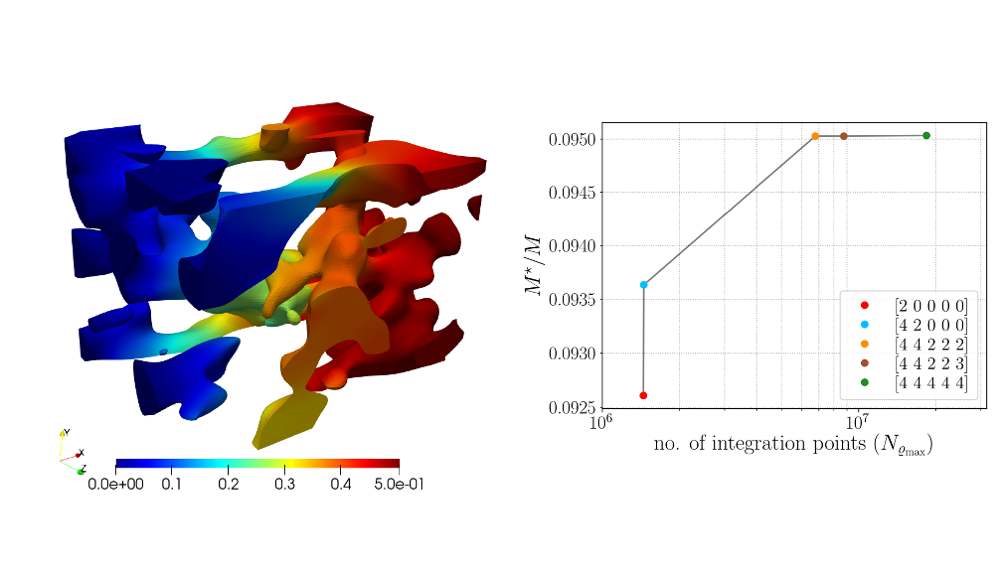
Fig. 3: Full integration vs adaptive integration of elongation of sintered glass
February 17th, 2020

