Multi-scale analyses are nowadays widely used to study the mechanical response of structures made of heterogeneous materials, characterized by nonlinear behavior. Two scales are considered the structural/macroscopic scale and the material/microscopic scale. At the material level analytical, semi-analytical homogenization schemes can be adopted. The main advantage of semi-analytical homogenization schemes is their significantly low computational effort, which comes at the expense of a limited accuracy, compared to computational homogenization approaches like the well-known FE2 method.
Reduced order methods, usually based on data analysis and clustering, provide an effective way to decrease the numerical effort of computational approaches. Worth mentioning are the Transformation Field Analysis (TFA) proposed by Dvorak (1992) and its evolutions (NTFA, PWUTFA, NUTFA).
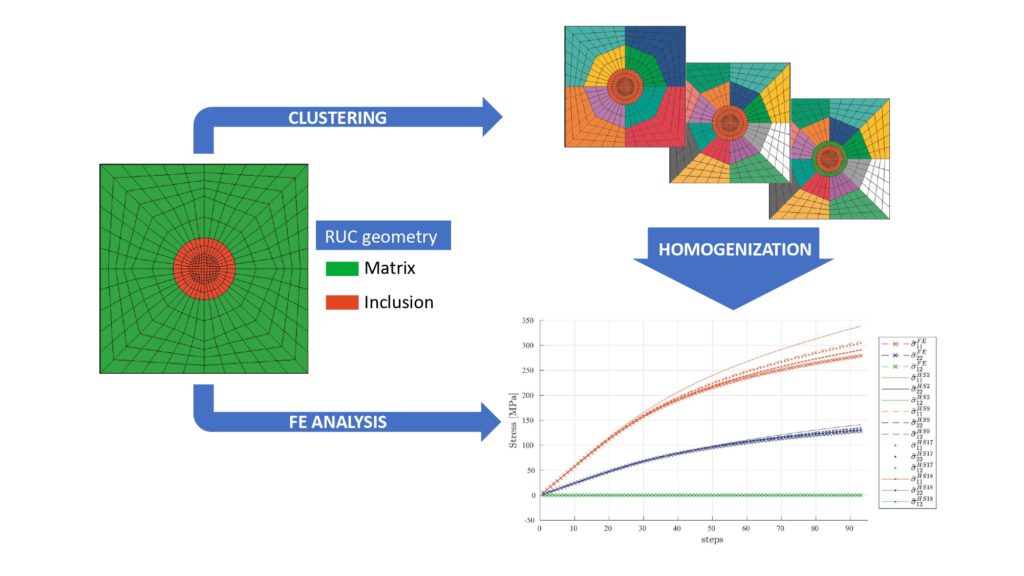
Our CompMech member, Alfredo Castrogiovanni, under the supervision of Prof. Ferdinando Auricchio and in collaboration with Prof. Elio Sacco (Università degli Studi di Napoli Federico II) and Prof. Sonia Marfia (Università degli Studi di Roma Tre), is working on a semi-analytical model order reduction strategy which interpolates between the Hashin-Shtrikman theory and a computational approach: a reference elastic medium coupled to the real multi-phase nonlinear material via an eigenstress field is introduced. Further, the RUC (Representative Unit Cell) is divided in a low number of regions called subsets, supposed to have a uniform strain; the local constitutive law is evaluated only once per subset leading to a drastic reduction of the global unknowns. The aim of our work is to predict the overall mechanical response of heterogeneous materials. The results obtained by the homogenization approach are compared with FE results.
May 27th, 2019

