Additive manufacturing is a potentially revolutionary technology, but its numerical simulation is challenging. In particular, the process exhibits localized dynamics across different scales, including phase change between the powder, liquid, and solid phase.
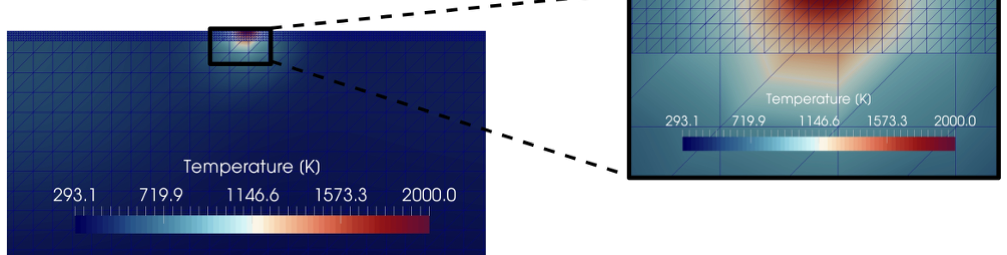
Components are constructed layer-by-layer, with each layer microns in length, however over the entire component important thermal and mechanical processes occur on the order of millimeters, as shown in Fig. 1.
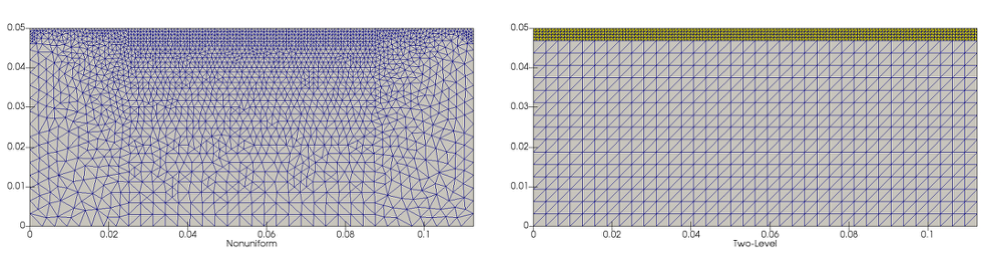
Although the difference in scale is large, the two scales interact heavily with each other, and so an effective simulation must effectively capture micrometer and millimeter scale behavior. A uniform mesh is therefore impossible.
Adding to the problem, the microscale region changes in time as the object is printed, making the use of fine uniform meshes difficult without implementing refinement-and-derefinement schemes. We propose instead to use a two-level method by splitting the mathematical problem into its fine scale and coarse scales, resolving the different problems on separate meshes.
This method allows us to use uniform meshes, and allows us to account for the evolving domain by simple translations. We have established a strong mathematical basis for the method, and its performance on test problems show it is computationally efficient. The method has been used to simulate full component construction efficiently on model problems and is being further developed in both the theoretical and practical directions.
More information can be found here: A. Viguerie, S. Bertoluzza and F. Auricchio. “A Fat boundary-type method for localized nonhomogenous material problems,” Computer Methods in Applied Mechanics and Engineering, 2020.
March 20th, 2020